|
DragonFire is a British laser directed-energy weapon (LDEW).
One kilometer is equal to 0.621371 miles (rounded to .62). To convert kilometers to miles, multiply the number of kilometers by 0.621371.
0 Comments
I post this video to help you understand the slope of a roof. It came up during the subpoenaed testimony of the Director of the US Secret Service, who resigned. My old HP calculator works fine for the calculations.
One improvement in school math is the introduction of algebra, geometry, and calculus concepts in early grades, usually 6th. I did not have that. One negative is common core. In general, it takes 20 minutes to solve a problem and five minutes the old way.
Most Americans understand nothing about a capitalist economy: supply and demand, micro, macro, statistics, inflation, government borrowing and debt, and low taxes and growth. Economics needs to be incorporated into math the same way algebra, geometry, and calculus are, early on, with real world examples. Standing alone, economics, not stats, is boring. problem: solution: real world example Owners defaulted. The value of the largest hotels dropped by $1B.
I showed the film, Modern Times, to a high school class, and one boy started laughing hysterically, which made me laugh harder. I had previewed it, but it wasn't until class that I really enjoyed it. Some pictures are a group experience. Siblings and friends, and I estimate 100 boys from the neighborhood, school, and sports, were physical with one another, and the only weapons we had were appendages. Loss of spontaneity is what accounts for so much isolation today.
This math problem generates his most exciting answer! Andy understands complementary angles and knows he can't eat in the gray areas because of two new pivot points. This is a hard SAT problem conceptually and for the time it takes to solve. On average, one minute is allowed for each SAT question. I met some goats, and one leaned against me. I didn't like that. I'm a city lad.
practical application
Let's say you have an above-ground water tank inside a rhombus-shaped fence and touching the fence at four tangent points. The tank is so big that you can't measure it, but you can walk the fence and measure it. Using Andy's formula, you can measure the size of the tank just by doing one more step. Use the formula for volume: multiple his answer by the height of the tank. You can eyeball that the way you measure tree height. I asked myself that question. Here is an excerpted answer:
A light beam is light which propagates essentially in one direction (directional light) and at the same time has a limited spatial extension in directions perpendicular to its beam direction. Often, it has a roughly circular cross-section but no precise spatial limitation. A light beam with circular cross-section may be characterized with a beam radius which generally changes during propagation. Over long enough distances, it must increase due to diffraction, since light is a wave phenomenon (→ wave optics). However, the beam radius may initially decrease before reaching a beam focus (or beam waist) where it has its minimum value. The increase in beam radius in the far field is associated with the beam divergence. A light beam can actually have two different focus positions e.g. for x and y direction; this is called astigmatism. https://www.rp-photonics.com/light_beams.html#:~:text=A%20light%20beam%20is%20light,but%20no%20precise%20spatial%20limitation. In the Basics of Space Flight, most abbreviations for units of measure are not spelled out the first time they are used, unlike the way other abbreviations are. See observable universe, a demonstration that uses the abbreviations, k and m:
https://science.nasa.gov/learn/basics-of-space-flight/units/ Destination: edge
Launch location: France Premise: take Earth there Time: Greenwich Mean Time Requirements: Greek and Latin Mission: go where no man has gone Naming heavenly bodies: license granted Optional: Hawaiian Laniakea immense heaven reaction: beautiful Homeschooling has the advantage. Here are the areas of math that interested me: numbers; basic math like word problems; algebra; and applied geometry. I would have been interested in some calculus if it were astronomy. An example would be trajectories, but that was not offered.
He pursues his interests.
During summer, students tend to forget math and English lessons from the school year that just ended. A list of novels for summer is great, but math teachers are remiss for not assigning math problems. As an example, I would assign one Algebra I problem in the following areas for each week of summer:
(7) Real-world examples: a) how many cans can be picked up given the size of the can and the capacity of the garbage truck? b) how many stiches are needed for a patient whose appendix has been removed? (Show work using variables.) Adobe stock image
What is a mode in music? It doesn't contain any notes but refers to how the intervals between the notes of a scale are arranged, a particular set of whole steps & half steps (white/black keys of a piano).
I need constant math reminders: Earth’s Population in Perspective
The population of Earth is around eight billion, an interesting figure. However, if you condense eight billion to 100 persons and then into various statistics, the resulting analysis is easier to comprehend. Out of 100: 11 are in Europe 5 are in North America 9 are in South America 15 are in Africa 60 are in Asia & Australia (Oceania) 49 live in the countryside 51 live in cities 75 have mobile phones 25 do not 30 have internet access 70 do not 83 can read 17 are illiterate 33 are Christians 22 are Muslims 14 are Hindus 7 are Buddhists 12 are other religions 12 have no religious beliefs 26 live less than 15 years 66 die between 15 and 64 8 are 65 and over If you own your home, eat full meals and drink clean water, have a mobile phone, can surf the internet, and have gone to college, you are in a privileged lot, less than seven percent. Archaeologists have demonstrated that humankind began in Africa. Here in the Americas, we are all immigrants, including so-called indigenous, and migration is an on-going process everywhere. Genesis gives us the story of God’s intentions.  The equilateral triangle is a symbol of the Holy Trinity. Also, there is the Celtic Trinity Knot opposite. Jacqueline of ahearttoknow.com says, “My daughter and I talked about how God is revealed to us as three different Persons. We labeled one loop as the Father, One as the Son, and One as the Holy Spirit.” And then there is the circle that excites Andy Math. I thought of myself and my parents on the same circle with the Holy Ghost at the center of the circle, not in a direct way, but that is how He came to me. It sounds wacky and tetched, but it really happened. See entry of 1/11/2024 on degenerate triangles where Prime Newtons mentions a square matrix. An explanation is complicated, so here is a look at a square matrix, Q.
I bet most people who had geometry in high school did not learn this. I will present these concepts to Alexander, 10, next time. Is light attracted by gravity? Answered on Quora by Kip Ingram, PhD in Electrical Engineering, The University of Texas at Austin, Cockrell School of Engineering (1992) Newton’s theory of gravity would have said “no,” and since Newton’s theory is the most people are generally exposed to in “early physics education” a lot of people walk around thinking that zero mass [light] implies no gravitational activity. This turns out to be incorrect, though for practical day-to-day calculations it’s perfectly good. Einstein gave us an improved theory of gravity in the early 1900’s, and under his theory any form of energy whatsoever both creates gravitational effects and responds to gravitational effects created by other things. Yes, light follows a curved path through a gravitational field that can be calculated using Einstein’s theory. Observation of this light curvature was the first “big confirmation” of Einstein’s new theory and was done using a solar eclipse to allow us to see starlight that passed close to the sun on its way to us. Those stars showed up in the “wrong positions,” but precisely where Einstein’s theory told us to expect to see them. 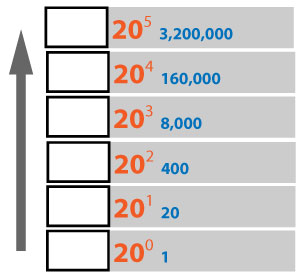 "My math teacher gave me an answer for why some ancient civilizations used a base-20, or vigesimal, math system: humans have 10 fingers and 10 toes." "There are 19 people in front of you in line, so you're in the vigesimal spot." "I have an affinity for all things vigesimal: I was born on June 20, I met my husband when I was 20, and my daughter was born on January 20." courtesy of worddaily.com mathmasterytutoring Latin - vīgintī If the average of 10% of a number, 25% of that number, 50% of that number, and 75% of that number is 24, what is the number? Where x is the unknown number...10% x + 25% (10% x) + 50% (25% x 10% x) + 75% (50% x 25% x 10% x)/4. The word of means multiplication. There are four values (10%, 25%, 50%, and 75%), so to get the average, divide by 4.
What are some real-world examples of the formula? Recipes. DIY's. If you got directions like that, you would call the customer service rep to complain, huh? Can you think of better examples? Algorithms have locked onto me because I am on the internet.
Can you explain simply the difference between an algorithm and a logarithm? Answered by Clem Cole, former HPC Arch, Consulting Engineer at Intel 2006–2023, Quora contributor. An algorithm is a process (set of instructions) to be followed to solve a problem…The term was used to define a set of calculations that a mathematician uses to get an answer to a problem. … When electronic calculating machines began to emerge in the late 1950s, early 1960s, the term ‘computer’ was reused to describe the machine that performed those processes, and the term ‘algorithm’ was reused to describe the programming (code) that these new type of computers used to perform the calculation. A logarithm is a mathematical property of a number; specifically, the quantity representing the power to which a fixed number, called the base, must be raised to produce a given number. … The giant property developer is on the verge of bankruptcy. https://www.bloomberg.com/news/videos/2023-12-03/china-evergrande-faces-final-chance-to-avoid-liquidation-video
|
Categories
All
Archives
July 2024
|
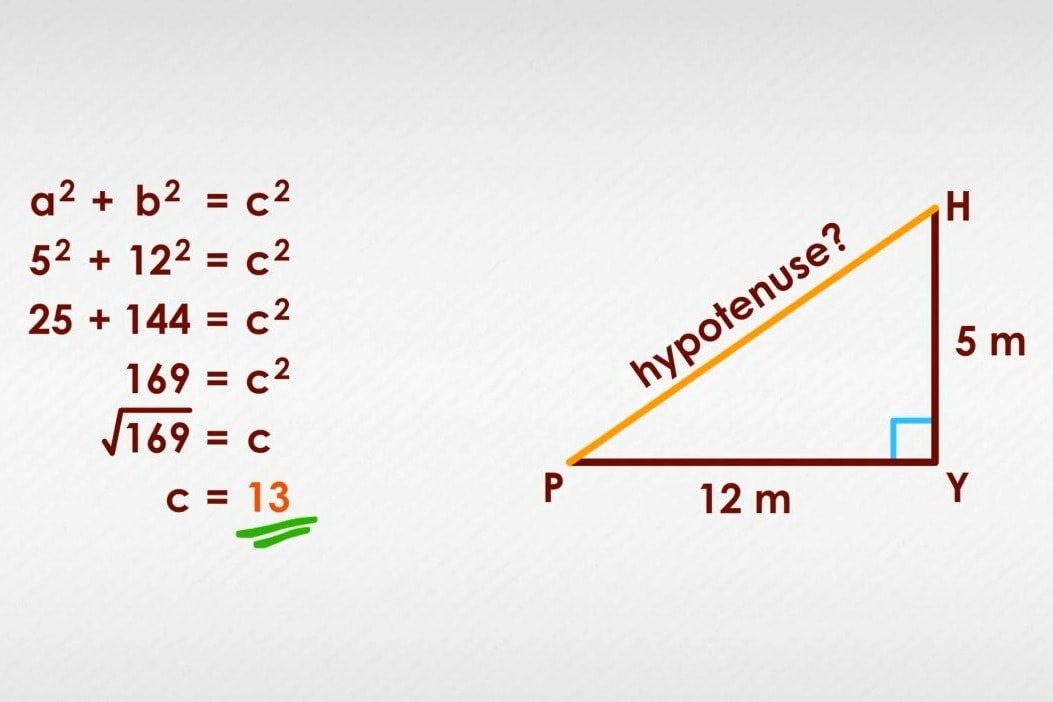

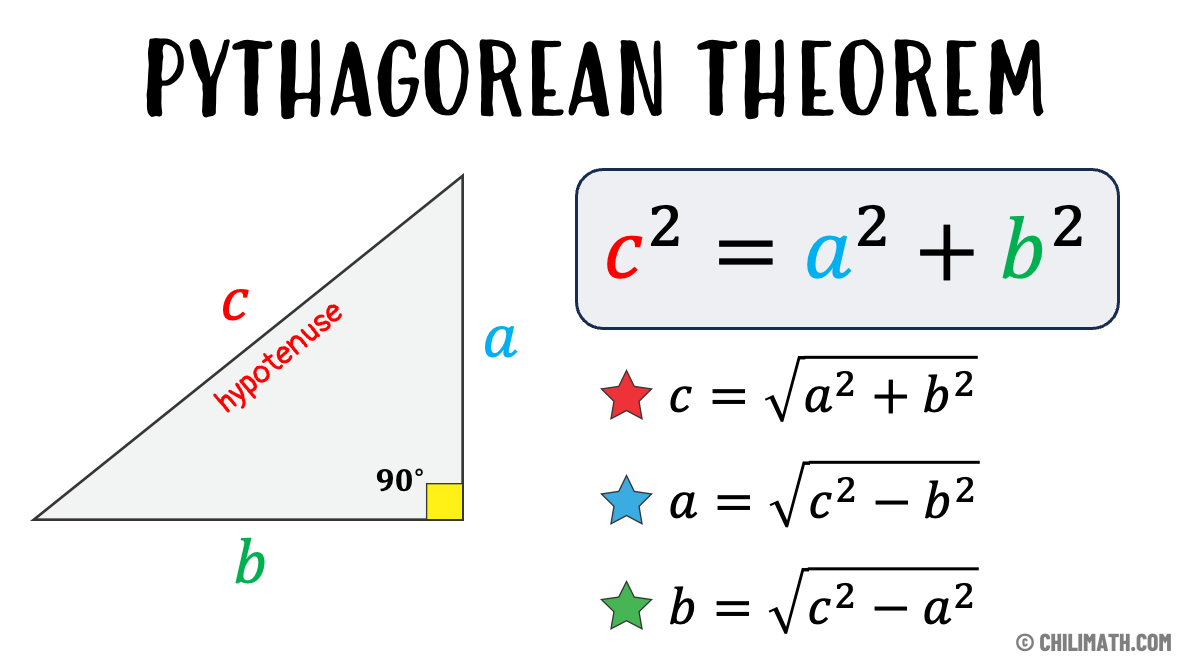
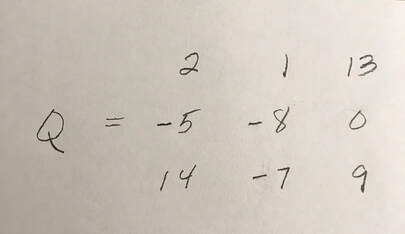
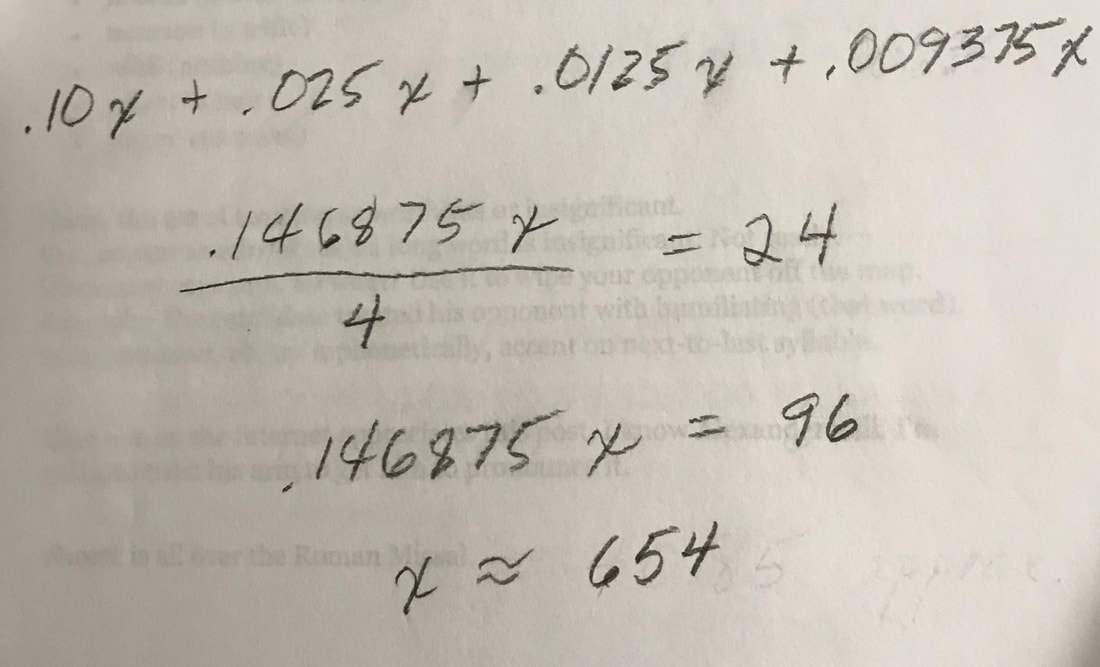
 RSS Feed
RSS Feed