degenerate tetrahedron

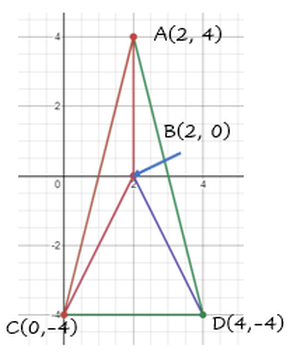
​What is the area of the tetrahedron with vertices (2,4) (2,0) (0,-4) (4,-4)?
 
Answered by Gary Ward, Quora, MaEd Education & Mathematics, Austin Peay State University (1997)

Label the vertices A (2,4), B (2,0), C (0,-4) and D (4,-4).

Since only two dimensions are given for a 3D figure, this is a degenerate tetrahedron with four faces ACD and ADB, DCB and CAB going clockwise.

Due to its unique geometry, the area of ACD = ADB + DCB + CAB, so the total area equals 2 · Area_ACD.

A = 2(½ · b · h) = 2(½ · 4 · 8) = 32 units²
​
Explanation of degenerate tetrahedron: Since a tetrahedron is a three-dimensional figure, count the area of all four faces, even though the volume is zero. If the question had just asked for the area of the figure meaning two-dimensional, it would be 16 units².

The total area of the degenerate tetrahedron is 32 square units.

There was one disagreeing voice on Quora. No matter. Gary taught me what a degenerate tetrahedron is. What is a tetrahedron? It is a solid having four plane triangular faces, which is a triangular pyramid, and Wikipedia has a nice gif of a rotating tetrahedron. ​https://en.wikipedia.org/wiki/Tetrahedron